What is Linear Algebra? - A First Course in Linear Algebra

We begin our study of linear algebra with an introduction and a motivational example.

Solving Systems of Linear Equations - A First Course in Linear Algebra

We will motivate our study of linear algebra by considering the problem of solving several linear equations simultaneously. The word solve tends to get abused somewhat, as in “solve this problem.” When talking about equations we understand a more precise meaning: find all of the values of some variable quantities that make an equation, or several equations, simultaneously true.

Solving Systems of Linear Equations - A First Course in Linear Algebra

We will motivate our study of linear algebra by considering the problem of solving several linear equations simultaneously. The word solve tends to get abused somewhat, as in “solve this problem.” When talking about equations we understand a more precise meaning: find all of the values of some variable quantities that make an equation, or several equations, simultaneously true.

Solving Systems of Linear Equations - A First Course in Linear Algebra

We will motivate our study of linear algebra by considering the problem of solving several linear equations simultaneously. The word solve tends to get abused somewhat, as in “solve this problem.” When talking about equations we understand a more precise meaning: find all of the values of some variable quantities that make an equation, or several equations, simultaneously true.

Using matrices to solve linear systems

Equivalence of systems of linear equations, row operations, corresponding matrices representing the linear systems

Solving Systems of Linear Equations - A First Course in Linear Algebra

We will motivate our study of linear algebra by considering the problem of solving several linear equations simultaneously. The word solve tends to get abused somewhat, as in “solve this problem.” When talking about equations we understand a more precise meaning: find all of the values of some variable quantities that make an equation, or several equations, simultaneously true.

Solving Systems of Linear Equations - A First Course in Linear Algebra

We will motivate our study of linear algebra by considering the problem of solving several linear equations simultaneously. The word solve tends to get abused somewhat, as in “solve this problem.” When talking about equations we understand a more precise meaning: find all of the values of some variable quantities that make an equation, or several equations, simultaneously true.

Solving Systems of Linear Equations - A First Course in Linear Algebra

We will motivate our study of linear algebra by considering the problem of solving several linear equations simultaneously. The word solve tends to get abused somewhat, as in “solve this problem.” When talking about equations we understand a more precise meaning: find all of the values of some variable quantities that make an equation, or several equations, simultaneously true.

Notation for matrix entries, size of a matrix, etc

Notation for matrix entries, diagonal matrix, square matrix, identity matrix, and zero matrix.

Vector Arithmetic

Definition of vector, equality of vectors, vector addition, and scalar vector multiplication. Geometric and algebraic properties of vector addition are discussed. (need a topic on vector addition is commutative and associative)

Vector Addition and Scalar Multiplication

University of Waterloo Math Online -

Vector Addition and Scalar Multiplication

Slides for the accompanying video from University of Waterloo.

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

Using matrices to solve linear systems

Equivalence of systems of linear equations, row operations, corresponding matrices representing the linear systems

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

When does a linear system have a unique solution?

A 3x3 system having a unique solution is solved by putting the augmented matrix in reduced row echelon form. A picture of three intersecting planes provides geometric intuition.

Echelon form

Definition of echelon form, reduction of a matrix to echelon form in order to compute solutions to systems of linear equations; definition of reduced row echelon form

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

Reduced Row-Echelon Form - A First Course in Linear Algebra

After solving a few systems of equations, you will recognize that it does not matter so much what we call our variables, as opposed to what numbers act as their coefficients. A system in the variables \(x_1,\,x_2,\,x_3\) would behave the same if we changed the names of the variables to \(a,\,b,\,c\) and kept all the constants the same and in the same places. In this section, we will isolate the key bits of information about a system of equations into something called a matrix, and then use this matrix to systematically solve the equations. Along the way we will obtain one of our most important and useful computational tools.

When does a linear system have a unique solution?

A 3x3 system having a unique solution is solved by putting the augmented matrix in reduced row echelon form. A picture of three intersecting planes provides geometric intuition.

Solution Sets

Sample problems to help understand when a linear system has 0, 1, or infinitely many solutions.

Types of Solution Sets - A First Course in Linear Algebra

We will now be more careful about analyzing the reduced row-echelon form derived from the augmented matrix of a system of linear equations. In particular, we will see how to systematically handle the situation when we have infinitely many solutions to a system, and we will prove that every system of linear equations has either zero, one or infinitely many solutions. With these tools, we will be able to routinely solve any linear system.

Types of Solution Sets - A First Course in Linear Algebra

We will now be more careful about analyzing the reduced row-echelon form derived from the augmented matrix of a system of linear equations. In particular, we will see how to systematically handle the situation when we have infinitely many solutions to a system, and we will prove that every system of linear equations has either zero, one or infinitely many solutions. With these tools, we will be able to routinely solve any linear system.

Types of Solution Sets - A First Course in Linear Algebra

We will now be more careful about analyzing the reduced row-echelon form derived from the augmented matrix of a system of linear equations. In particular, we will see how to systematically handle the situation when we have infinitely many solutions to a system, and we will prove that every system of linear equations has either zero, one or infinitely many solutions. With these tools, we will be able to routinely solve any linear system.

Types of Solution Sets - A First Course in Linear Algebra

We will now be more careful about analyzing the reduced row-echelon form derived from the augmented matrix of a system of linear equations. In particular, we will see how to systematically handle the situation when we have infinitely many solutions to a system, and we will prove that every system of linear equations has either zero, one or infinitely many solutions. With these tools, we will be able to routinely solve any linear system.

When does a linear system have a unique solution?

A 3x3 system having a unique solution is solved by putting the augmented matrix in reduced row echelon form. A picture of three intersecting planes provides geometric intuition.

Solution Sets

Sample problems to help understand when a linear system has 0, 1, or infinitely many solutions.

Types of Solution Sets - A First Course in Linear Algebra

We will now be more careful about analyzing the reduced row-echelon form derived from the augmented matrix of a system of linear equations. In particular, we will see how to systematically handle the situation when we have infinitely many solutions to a system, and we will prove that every system of linear equations has either zero, one or infinitely many solutions. With these tools, we will be able to routinely solve any linear system.

Types of Solution Sets - A First Course in Linear Algebra

We will now be more careful about analyzing the reduced row-echelon form derived from the augmented matrix of a system of linear equations. In particular, we will see how to systematically handle the situation when we have infinitely many solutions to a system, and we will prove that every system of linear equations has either zero, one or infinitely many solutions. With these tools, we will be able to routinely solve any linear system.

Types of Solution Sets - A First Course in Linear Algebra

We will now be more careful about analyzing the reduced row-echelon form derived from the augmented matrix of a system of linear equations. In particular, we will see how to systematically handle the situation when we have infinitely many solutions to a system, and we will prove that every system of linear equations has either zero, one or infinitely many solutions. With these tools, we will be able to routinely solve any linear system.

Finding all solutions of systems of linear equations

How to compute all solutions to a general system $Ax=b$ of linear equations and connection to the corresponding homogeneous system $Ax=0$. Visualization of the geometry of solution sets. Consistent systems and their solution using row reduction.

Solving homogeneous systems of equations

Homogeneous systems of linear equations; trivial versus nontrivial solutions of homogeneous systems; how to find nontrivial solutions; how to know from the reduced row-echelon form of a matrix whether the corresponding homogeneous system has nontrivial solutions.

Homogeneous Systems of Equations - A First Course in Linear Algebra

In this section we specialize to systems of linear equations where every equation has a zero as its constant term. Along the way, we will begin to express more and more ideas in the language of matrices and begin a move away from writing out whole systems of equations. The ideas initiated in this section will carry through the remainder of the course.

Homogeneous Systems of Equations - A First Course in Linear Algebra

In this section we specialize to systems of linear equations where every equation has a zero as its constant term. Along the way, we will begin to express more and more ideas in the language of matrices and begin a move away from writing out whole systems of equations. The ideas initiated in this section will carry through the remainder of the course.

Homogeneous Systems of Equations - A First Course in Linear Algebra

In this section we specialize to systems of linear equations where every equation has a zero as its constant term. Along the way, we will begin to express more and more ideas in the language of matrices and begin a move away from writing out whole systems of equations. The ideas initiated in this section will carry through the remainder of the course.

Homogeneous Systems of Equations - A First Course in Linear Algebra

In this section we specialize to systems of linear equations where every equation has a zero as its constant term. Along the way, we will begin to express more and more ideas in the language of matrices and begin a move away from writing out whole systems of equations. The ideas initiated in this section will carry through the remainder of the course.

Homogeneous Systems of Equations - A First Course in Linear Algebra

In this section we specialize to systems of linear equations where every equation has a zero as its constant term. Along the way, we will begin to express more and more ideas in the language of matrices and begin a move away from writing out whole systems of equations. The ideas initiated in this section will carry through the remainder of the course.

The Matrix Inverse - Definition

Motivation and definition of the inverse of a matrix

Notation for matrix entries, size of a matrix, etc

Notation for matrix entries, diagonal matrix, square matrix, identity matrix, and zero matrix.

Matrix Inverse

The definition of matrix inverse is motivated by considering multiplicative inverse. The identity matrix and matrix inverse are defined.

Invertible Matrix Theorem

Statements that are equivalent to a square matrix being invertible; examples.

Matrix inverses

Properties of matrix inversion: inverse of the inverse, inverse of the transpose, inverse of a product; elementary matrices and corresponding row operations; a matrix is invertible if and only if it is row-equivalent to the identity matrix; row-reduction algorithm for computing matrix inverse

Nonsingular Matrices - A First Course in Linear Algebra

In this section we specialize further and consider matrices with equal numbers of rows and columns, which when considered as coefficient matrices lead to systems with equal numbers of equations and variables. We will see in the second half of the course (Chapter D, Chapter E, Chapter LT, Chapter R) that these matrices are especially important.

Nonsingular Matrices - A First Course in Linear Algebra

In this section we specialize further and consider matrices with equal numbers of rows and columns, which when considered as coefficient matrices lead to systems with equal numbers of equations and variables. We will see in the second half of the course (Chapter D, Chapter E, Chapter LT, Chapter R) that these matrices are especially important.

Nonsingular Matrices - A First Course in Linear Algebra

In this section we specialize further and consider matrices with equal numbers of rows and columns, which when considered as coefficient matrices lead to systems with equal numbers of equations and variables. We will see in the second half of the course (Chapter D, Chapter E, Chapter LT, Chapter R) that these matrices are especially important.

Nonsingular Matrices - A First Course in Linear Algebra

In this section we specialize further and consider matrices with equal numbers of rows and columns, which when considered as coefficient matrices lead to systems with equal numbers of equations and variables. We will see in the second half of the course (Chapter D, Chapter E, Chapter LT, Chapter R) that these matrices are especially important.

Nonsingular Matrices - A First Course in Linear Algebra

In this section we specialize further and consider matrices with equal numbers of rows and columns, which when considered as coefficient matrices lead to systems with equal numbers of equations and variables. We will see in the second half of the course (Chapter D, Chapter E, Chapter LT, Chapter R) that these matrices are especially important.

Nonsingular Matrices - A First Course in Linear Algebra

In this section we specialize further and consider matrices with equal numbers of rows and columns, which when considered as coefficient matrices lead to systems with equal numbers of equations and variables. We will see in the second half of the course (Chapter D, Chapter E, Chapter LT, Chapter R) that these matrices are especially important.

Nonsingular Matrices - A First Course in Linear Algebra

In this section we specialize further and consider matrices with equal numbers of rows and columns, which when considered as coefficient matrices lead to systems with equal numbers of equations and variables. We will see in the second half of the course (Chapter D, Chapter E, Chapter LT, Chapter R) that these matrices are especially important.

Vector Arithmetic

Definition of vector, equality of vectors, vector addition, and scalar vector multiplication. Geometric and algebraic properties of vector addition are discussed. (need a topic on vector addition is commutative and associative)

Vector Addition and Scalar Multiplication

University of Waterloo Math Online -

Vector Addition and Scalar Multiplication

Slides for the accompanying video from University of Waterloo.

Vector Addition and Scalar Multiplication Quiz

Quiz from the University of Waterloo.

Vector Operations - A First Course in Linear Algebra

In this section we define some new operations involving vectors, and collect some basic properties of these operations. Begin by recalling our definition of a column vector as an ordered list of complex numbers, written vertically (Definition CV). The collection of all possible vectors of a fixed size is a commonly used set, so we start with its definition.

Vector Operations - A First Course in Linear Algebra

In this section we define some new operations involving vectors, and collect some basic properties of these operations. Begin by recalling our definition of a column vector as an ordered list of complex numbers, written vertically (Definition CV). The collection of all possible vectors of a fixed size is a commonly used set, so we start with its definition.

Vector Operations - A First Course in Linear Algebra

In this section we define some new operations involving vectors, and collect some basic properties of these operations. Begin by recalling our definition of a column vector as an ordered list of complex numbers, written vertically (Definition CV). The collection of all possible vectors of a fixed size is a commonly used set, so we start with its definition.

Vector Operations - A First Course in Linear Algebra

In this section we define some new operations involving vectors, and collect some basic properties of these operations. Begin by recalling our definition of a column vector as an ordered list of complex numbers, written vertically (Definition CV). The collection of all possible vectors of a fixed size is a commonly used set, so we start with its definition.

Vector Operations - A First Course in Linear Algebra

In this section we define some new operations involving vectors, and collect some basic properties of these operations. Begin by recalling our definition of a column vector as an ordered list of complex numbers, written vertically (Definition CV). The collection of all possible vectors of a fixed size is a commonly used set, so we start with its definition.

Matrix equations as motivation for basis and span

Advice to instructors for in-class activities on matrix-vector multiplication and translating between the various equivalent notation forms of linear systems, and suggestions for how this topic can be used to motivate future topics.

Matrix equations with zero or infinitely many solutions

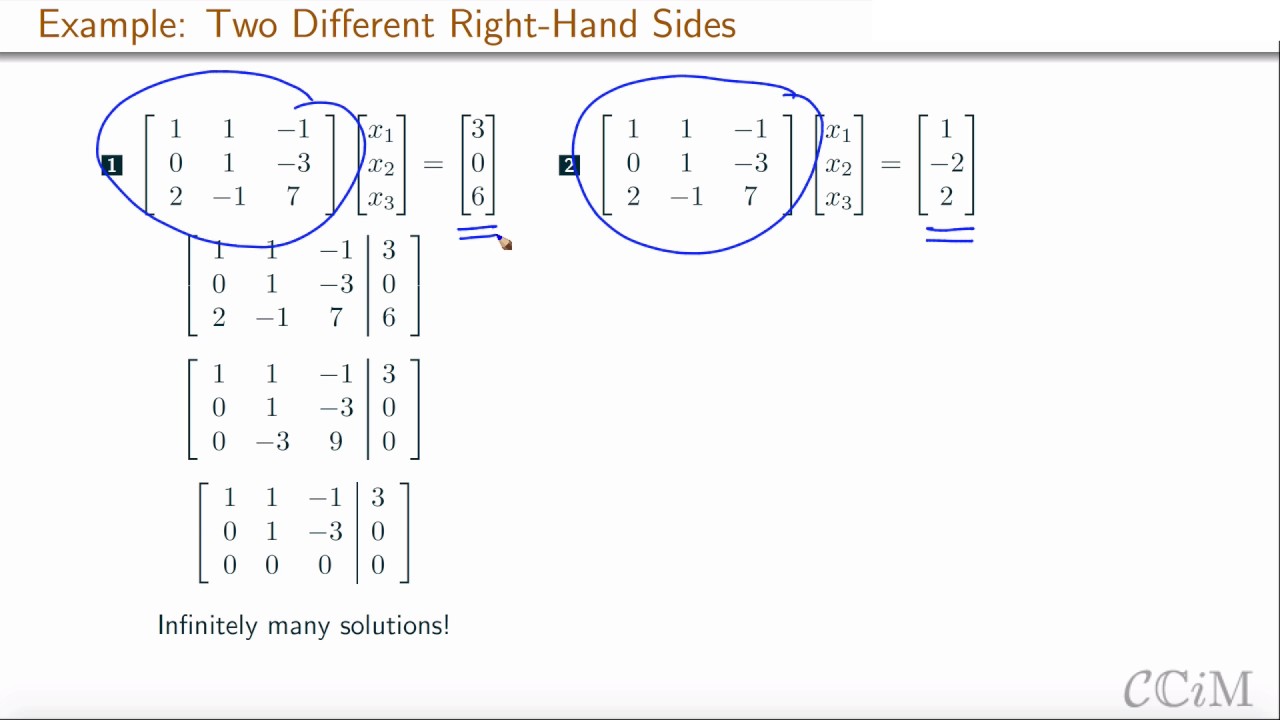
A 3x3 matrix equation Ax=b is solved for two different values of b. In one case there is no solution, and in another there are infinitely many solutions. These examples illustrate a theorem about linear combinations of the columns of the matrix A.

Linear combinations of vectors

The linear combination of a set of vectors is defined. Determine if a vector in R^2 is in the span of two other vectors. The span of a set of vectors is related to the columns of a matrix. (need topic: Determine if a vector in R^2 is in the span of two other vectors.)

Span of a set of vectors

Definition of the span of a set of vectors. Example of checking if a vector in R^3 is in the span of a set of two vectors. Geometric picture of a span.

Vector Equations: In-Class Activities

Suggestions for in-class activities on linear combination and span of vectors in R^n. (need a topic for the general *process* of determining if a vector is in the span of a set of devtors)

Linear Combinations and Span

In-class activity for linear combinations and span.

Vector Addition and Scalar Multiplication

University of Waterloo Math Online -

Matrix equations and spanning sets

Equivalent statements for a matrix A: for every right-hand side b, the system Ax=b has a solution; every b is a linear combination of the columns of A; the span of the columns of A is maximal; A has a pivot position in every row.

Linear Combinations - A First Course in Linear Algebra

In Section VO we defined vector addition and scalar multiplication. These two operations combine nicely to give us a construction known as a linear combination, a construct that we will work with throughout this course.

Linear Combinations - A First Course in Linear Algebra

In Section VO we defined vector addition and scalar multiplication. These two operations combine nicely to give us a construction known as a linear combination, a construct that we will work with throughout this course.

Column and Row Spaces - A First Course in Linear Algebra

A matrix-vector product (Definition MVP) is a linear combination of the columns of the matrix and this allows us to connect matrix multiplication with systems of equations via Theorem SLSLC. Row operations are linear combinations of the rows of a matrix, and of course, reduced row-echelon form (Definition RREF) is also intimately related to solving systems of equations. In this section we will formalize these ideas with two key definitions of sets of vectors derived from a matrix.

Linear Combinations - A First Course in Linear Algebra

In Section VO we defined vector addition and scalar multiplication. These two operations combine nicely to give us a construction known as a linear combination, a construct that we will work with throughout this course.

Linear Combinations - A First Course in Linear Algebra

In Section VO we defined vector addition and scalar multiplication. These two operations combine nicely to give us a construction known as a linear combination, a construct that we will work with throughout this course.

Span of a set of vectors

Definition of the span of a set of vectors. Example of checking if a vector in R^3 is in the span of a set of two vectors. Geometric picture of a span.

Vector Equations: In-Class Activities

Suggestions for in-class activities on linear combination and span of vectors in R^n. (need a topic for the general *process* of determining if a vector is in the span of a set of devtors)

Linear Combinations and Span

In-class activity for linear combinations and span.

Properties of Vectors and Spanning

From the University of Waterloo Math Online

Properties of Vectors and Spanning

Slides from the corresponding video from the University of Waterloo.

Spanning Sets - A First Course in Linear Algebra

In this section we will provide an extremely compact way to describe an infinite set of vectors, making use of linear combinations. This will give us a convenient way to describe the solution set of a linear system, the null space of a matrix, and many other sets of vectors.

Span of a set of vectors

Definition of the span of a set of vectors. Example of checking if a vector in R^3 is in the span of a set of two vectors. Geometric picture of a span.

Vector Equations: In-Class Activities

Suggestions for in-class activities on linear combination and span of vectors in R^n. (need a topic for the general *process* of determining if a vector is in the span of a set of devtors)

Linear Combinations and Span

In-class activity for linear combinations and span.

Properties of Vectors and Spanning

From the University of Waterloo Math Online

Properties of Vectors and Spanning

Slides from the corresponding video from the University of Waterloo.

Spanning Sets - A First Course in Linear Algebra

In this section we will provide an extremely compact way to describe an infinite set of vectors, making use of linear combinations. This will give us a convenient way to describe the solution set of a linear system, the null space of a matrix, and many other sets of vectors.

Spanning Sets - A First Course in Linear Algebra

In this section we will provide an extremely compact way to describe an infinite set of vectors, making use of linear combinations. This will give us a convenient way to describe the solution set of a linear system, the null space of a matrix, and many other sets of vectors.

How to find out if a set of vectors is linearly independent?

Linear independence is defined, followed by a worked example of 3 vectors in R^3.

Linear Independence in-class activity

Linear independence in-class activity

University of Waterloo Math Online - Lesson: Linear Independence and Surfaces

Video Lesson from University of Waterloo.

Vector Addition and Scalar Multiplication Quiz

Quiz from the University of Waterloo.

Linear Independence - A First Course in Linear Algebra

Linear independence is one of the most fundamental conceptual ideas in linear algebra, along with the notion of a span. So this section, and the subsequent Section LDS, will explore this new idea.

Linear Independence - A First Course in Linear Algebra

Linear independence is one of the most fundamental conceptual ideas in linear algebra, along with the notion of a span. So this section, and the subsequent Section LDS, will explore this new idea.

Linear Independence - A First Course in Linear Algebra

Linear independence is one of the most fundamental conceptual ideas in linear algebra, along with the notion of a span. So this section, and the subsequent Section LDS, will explore this new idea.

Linear Independence - A First Course in Linear Algebra

Linear independence is one of the most fundamental conceptual ideas in linear algebra, along with the notion of a span. So this section, and the subsequent Section LDS, will explore this new idea.

Linear Independence - A First Course in Linear Algebra

Linear independence is one of the most fundamental conceptual ideas in linear algebra, along with the notion of a span. So this section, and the subsequent Section LDS, will explore this new idea.

Linear Independence - A First Course in Linear Algebra

Linear independence is one of the most fundamental conceptual ideas in linear algebra, along with the notion of a span. So this section, and the subsequent Section LDS, will explore this new idea.

Linear Independence - A First Course in Linear Algebra

Linear independence is one of the most fundamental conceptual ideas in linear algebra, along with the notion of a span. So this section, and the subsequent Section LDS, will explore this new idea.

Linear Independence - A First Course in Linear Algebra

Linear independence is one of the most fundamental conceptual ideas in linear algebra, along with the notion of a span. So this section, and the subsequent Section LDS, will explore this new idea.

Linear Independence in-class activity

Linear independence in-class activity

University of Waterloo Math Online - Lesson: Linear Independence and Surfaces

Video Lesson from University of Waterloo.

Vector Addition and Scalar Multiplication Quiz

Quiz from the University of Waterloo.

Linear Dependence and Spans - A First Course in Linear Algebra

In any linearly dependent set there is always one vector that can be written as a linear combination of the others. This is the substance of the upcoming Theorem DLDS. Perhaps this will explain the use of the word “dependent.” In a linearly dependent set, at least one vector “depends” on the others (via a linear combination).

Linear Dependence and Spans - A First Course in Linear Algebra

In any linearly dependent set there is always one vector that can be written as a linear combination of the others. This is the substance of the upcoming Theorem DLDS. Perhaps this will explain the use of the word “dependent.” In a linearly dependent set, at least one vector “depends” on the others (via a linear combination).

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Dot Product and Cross Product Lesson

This is a video from the University of Waterloo. Dot Product, Cross-Product in R^n (which should be in Chapter 8 section 4 about hyperplanes.

Dot Product, Cross Product, and Scalar Equations Quiz

Quiz from the University of Waterloo. This is intended to be used after the video of the same name.

Inner products and distance

Inner product of two vectors in R^n, length of a vector in R^n, orthogonality. Motivation via approximate solutions of systems of linear equations, definition and properties of inner product (symmetric, bilinar, positive definite); length/norm of a vector, unit vectors; definition of distance between vectors; definition of orthogonality; Pythagorean Theorem.

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Dot Product and Cross Product Lesson

This is a video from the University of Waterloo. Dot Product, Cross-Product in R^n (which should be in Chapter 8 section 4 about hyperplanes.

Dot Product, Cross Product, and Scalar Equations Quiz

Quiz from the University of Waterloo. This is intended to be used after the video of the same name.

Inner products and distance

Inner product of two vectors in R^n, length of a vector in R^n, orthogonality. Motivation via approximate solutions of systems of linear equations, definition and properties of inner product (symmetric, bilinar, positive definite); length/norm of a vector, unit vectors; definition of distance between vectors; definition of orthogonality; Pythagorean Theorem.

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthonormality

Orthonormal sets and bases (definition); expressing vectors as linear combinations of orthonormal basis vectors; matrices with orthonormal columns preserve vector norm and dot product; orthogonal matrices; inverse of an orthogonal matrix equals its transpose

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Orthogonality - A First Course in Linear Algebra

In this section we define a couple more operations with vectors, and prove a few theorems. At first blush these definitions and results will not appear central to what follows, but we will make use of them at key points in the remainder of the course (such as Section MINM, Section OD). Because we have chosen to use \(\complexes\) as our set of scalars, this subsection is a bit more, uh, … complex than it would be for the real numbers. We will explain as we go along how things get easier for the real numbers \({\mathbb R}\text{.}\) If you have not already, now would be a good time to review some of the basic properties of arithmetic with complex numbers described in Section CNO. With that done, we can extend the basics of complex number arithmetic to our study of vectors in \(\complex{m}\text{.}\)

Matrix Equation: Matrix-Vector Product

The product of a matrix times a vector is defined, and used to show that a system of linear equations is equivalent to a system of linear equations involving matrices and vectors. The example uses a 2x3 system.

Matrix Operations: Sums Scalar Multiplication

Definition of sum of matrices, product of a scalar and a matrix

In-class activities for matrix operations

Suggestions for in-class activities on matrix operations: addition, multiplication, transpose, and the fact that multiplication is not commutative.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Vector Spaces - A First Course in Linear Algebra

In this section we present a formal definition of a vector space, which will lead to an extra increment of abstraction. Once defined, we study its most basic properties.

Definition and properties of matrix transpose

The transpose of a matrix is defined, and various properties are explored using numerical examples.

Matrix operations

Associative and distributive properties of matrix multiplication and addition; multiplication by the identity matrix; definition of the transpose of a matrix; transpose of the transpose, transpose of a sum, transpose of a product

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Operations - A First Course in Linear Algebra

In this section we will back up and start simple. We begin with a definition of a totally general set of matrices, and see where that takes us.

Matrix Equation: Matrix-Vector Product

The product of a matrix times a vector is defined, and used to show that a system of linear equations is equivalent to a system of linear equations involving matrices and vectors. The example uses a 2x3 system.

Matrix equations as motivation for basis and span

Advice to instructors for in-class activities on matrix-vector multiplication and translating between the various equivalent notation forms of linear systems, and suggestions for how this topic can be used to motivate future topics.

How to multiply matrices

Learning goals: 1. What are the dimension (size) requirements for two matrices so that they can be multiplied to each other? 2. What is the product of two matrices, when it exists?

Matrix Multiplication - A First Course in Linear Algebra

We know how to add vectors and how to multiply them by scalars. Together, these operations give us the possibility of making linear combinations. Similarly, we know how to add matrices and how to multiply matrices by scalars. In this section we mix all these ideas together and produce an operation known as matrix multiplication. This will lead to some results that are both surprising and central. We begin with a definition of how to multiply a vector by a matrix.

Matrix Multiplication - A First Course in Linear Algebra

We know how to add vectors and how to multiply them by scalars. Together, these operations give us the possibility of making linear combinations. Similarly, we know how to add matrices and how to multiply matrices by scalars. In this section we mix all these ideas together and produce an operation known as matrix multiplication. This will lead to some results that are both surprising and central. We begin with a definition of how to multiply a vector by a matrix.

Matrix Multiplication - A First Course in Linear Algebra

We know how to add vectors and how to multiply them by scalars. Together, these operations give us the possibility of making linear combinations. Similarly, we know how to add matrices and how to multiply matrices by scalars. In this section we mix all these ideas together and produce an operation known as matrix multiplication. This will lead to some results that are both surprising and central. We begin with a definition of how to multiply a vector by a matrix.

How to multiply matrices

Learning goals: 1. What are the dimension (size) requirements for two matrices so that they can be multiplied to each other? 2. What is the product of two matrices, when it exists?

Matrix Multiplication - A First Course in Linear Algebra

We know how to add vectors and how to multiply them by scalars. Together, these operations give us the possibility of making linear combinations. Similarly, we know how to add matrices and how to multiply matrices by scalars. In this section we mix all these ideas together and produce an operation known as matrix multiplication. This will lead to some results that are both surprising and central. We begin with a definition of how to multiply a vector by a matrix.

Matrix Multiplication - A First Course in Linear Algebra

We know how to add vectors and how to multiply them by scalars. Together, these operations give us the possibility of making linear combinations. Similarly, we know how to add matrices and how to multiply matrices by scalars. In this section we mix all these ideas together and produce an operation known as matrix multiplication. This will lead to some results that are both surprising and central. We begin with a definition of how to multiply a vector by a matrix.

Matrix Multiplication - A First Course in Linear Algebra

We know how to add vectors and how to multiply them by scalars. Together, these operations give us the possibility of making linear combinations. Similarly, we know how to add matrices and how to multiply matrices by scalars. In this section we mix all these ideas together and produce an operation known as matrix multiplication. This will lead to some results that are both surprising and central. We begin with a definition of how to multiply a vector by a matrix.

Definition and properties of matrix transpose

The transpose of a matrix is defined, and various properties are explored using numerical examples.

Matrix Inverse

The definition of matrix inverse is motivated by considering multiplicative inverse. The identity matrix and matrix inverse are defined.

Matrix operations

Associative and distributive properties of matrix multiplication and addition; multiplication by the identity matrix; definition of the transpose of a matrix; transpose of the transpose, transpose of a sum, transpose of a product